同餘 (Congruence)

(好像我以前同學的名字 XD)

• a ≡ b (mod m) 表示 a 和 b 在以 m 為模數時，除以 m 的餘數相等。
  數學表示為：
  a ≡ b (mod m) ⇔ a % m = b % m (讀作 a mod m= b mod m)

• a ≡ 0 (mod m) 表示 a 可以被 m 整除。
  數學表示為：
  a ≡ 0 (mod m) ⇔ a % m = 0

模運算 (Modular Arithmetic)

• 是一種特殊的運算方式，它只關注數字除以某個數（模數）後的餘數。

• 模數的用途: 將大數轉化為小數，以方便進行分類和運算。

• 同餘的因數定理:
  如果 a ≡ b (mod k)，則 k 可以整除 a - b。
  數學表示為：
  a ≡ b (mod k) ⇔ k | (a - b)

• 同餘的加法性質:
  如果 a ≡ b (mod k) 且 c ≡ d (mod k)，則 a + c ≡ b + d (mod k)。
  數學表示為：
  a ≡ b (mod k) 且 c ≡ d (mod k) ⇔ a + c ≡ b + d (mod k)

• 同餘的乘法性質:
  如果 a ≡ b (mod k) 且 c ≡ d (mod k)，則 ac ≡ bd (mod k)。
  數學表示為：
  a ≡ b (mod k) 且 c ≡ d (mod k) ⇔ ac ≡ bd (mod k)

• 同餘的冪次性質:
  如果 a ≡ b (mod k)，則 a^n ≡ b^n (mod k)。
  數學表示為：
  a ≡ b (mod k) ⇔ a^n ≡ b^n (mod k)

• 同餘的倍數性質:
  如果 a ≡ b (mod k)，則 am ≡ bm (mod k)。
  數學表示為：
  a ≡ b (mod k) ⇔ am ≡ bm (mod k)

Modular-1

https://cryptohack.org/courses/modular/ma0/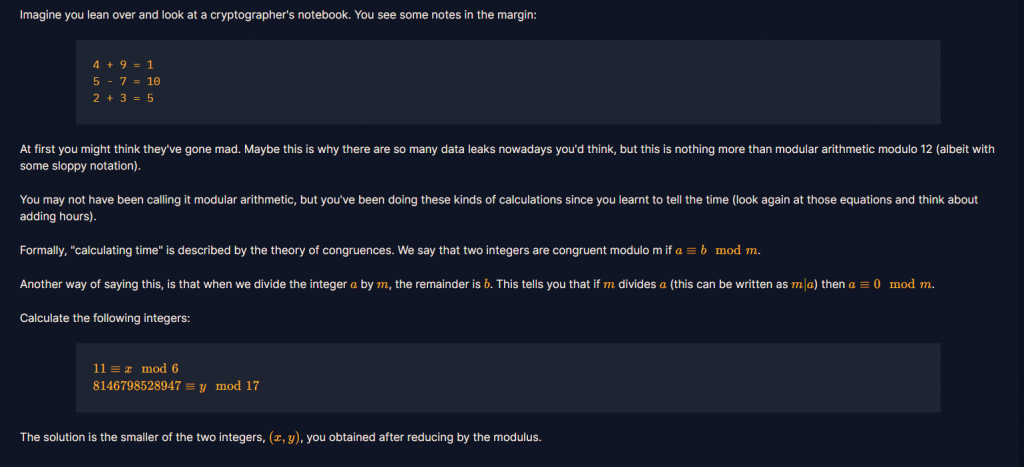

題意:

介紹模數運算的概念，並用計算時間作比喻。
在12小時制中，我們其實就是在進行模12的運算，任何一個整數，除以12後的餘數，就是它在模12系統下的值。所 以13點為1點，14點為2點。

題目給了我們兩條 mod 運算式:
11 ≡ x mod 6
8146798528947 ≡ y mod 17
而我們需要返回的答案就是x和y中較小的那個值。

程式碼:

我們只需要分別求出 11 mod 6 和 8146798528947 mod 17 的值，就能得出x和y。

# 11≡xmod6
# 8146798528947≡ymod17
x=11%6
y=8146798528947%17
print(min(x,y))

4

參考資料:

同餘:

• wiki: https://zh.wikipedia.org/zh-tw/%E5%90%8C%E9%A4%98

模運算:

• wiki: https://zh.wikipedia.org/zh-tw/%E6%A8%A1%E7%AE%97%E6%95%B8
• 詳細的內容: https://ithelp.ithome.com.tw/articles/10205727

後話:

今天查閱了同餘、模運算的相關內容，本來要順便放Modular-4的東西，但因為涉及到環、域以及費馬小定理，內容較多，所以明天再寫吧。